This course and its exam closed on August 18, 2018. It is no longer possible to enroll in or obtain a certificate for this course.
Course Introduction
This course is designed to introduce you to the study of calculus. You will learn concrete applications of how calculus is used and, more importantly, why it works. Calculus is not a new discipline; it has been around since the days of Archimedes. However, Isaac Newton and Gottfried Leibniz, two seventeenth-century European mathematicians concurrently working on the same intellectual discovery hundreds of miles apart, were responsible for developing the field as we know it today. This brings us to our first question, what is today's calculus? In its simplest terms, calculus is the study of functions, rates of change, and continuity. While you may have cultivated a basic understanding of functions in previous math courses, in this course you will come to a more advanced understanding of their complexity, learning to take a closer look at their behaviors and nuances. In this course, we will address three major topics: limits, derivatives, and integrals, as well as study their respective foundations and applications. By the end of this course, you will have a solid understanding of the behavior of functions and graphs. Whether you are entirely new to calculus or just looking for a refresher on a particular topic, this course has something to offer, balancing computational proficiency with conceptual depth.
Unit 1: Analytic Geometry
Most of the material in this unit will be review. However, the notions of points, lines, circles, distance, and functions will be central in everything that follows. Lines are basic geometric objects which will be of great importance in the study of differential calculus, particularly in the study of tangent lines and linear approximations.
We will also take a look at the practical uses of mathematical functions. This course will use mathematical models, or structures, that predict practical situations in order to describe and study a number of real-life problems and situations. They are essential to the development of every major business and every scientific field in the modern world.
Completing this unit should take you approximately 9 hours.
Unit 2: Instantaneous Rate of Change: The Derivative
In this unit, you will study the instantaneous rate of change of a function. Motivated by this concept, you will develop the notion of limits, continuity, and the derivative. The limit asks the question, 'What does the function do as the independent variable becomes closer and closer to a certain value?' In simpler terms, the limit is the natural tendency of a function. The limit is incredibly important due to its relationship to the derivative, the integral, and countless other key mathematical concepts. A strong understanding of the limit is essential to success in the field of mathematics.
A derivative is a description of how a function changes as its input varies. In the case of a straight line, this derivative, or slope, is the same at every point, which is why we can describe the slope of an entire function with one number when it is linear. You will learn that we can do the same for nonlinear functions. The slope, however, will not be constant; it will change as the independent variable changes.
Completing this unit should take you approximately 16 hours.
Unit 3: Rules for Finding Derivatives
Computing a derivative requires the computation of a limit. Because limit computations can be rather involved, we like to minimize the amount of work we have to do in practice. In this unit, we build up some rules for differentiation which will speed up our calculations of derivatives. In particular, you will see how to differentiate the sum, difference, product, quotient, and composition of two (or more) functions. You will also learn rules for differentiating power functions (including polynomial and root functions).
Completing this unit should take you approximately 12 hours.
Unit 4: Transcendental Functions
In this unit, you will investigate the derivatives of trigonometric, inverse trigonometric, exponential, and logarithmic functions. Along the way, you will develop a technique of differentiation called implicit differentiation. Aside from allowing you to compute derivatives of inverse function, implicit differentiation will also be important in studying related rates problems later on.
Completing this unit should take you approximately 17 hours.
Unit 5: Curve Sketching
This unit will ask you to apply a little critical thinking to the topics this course has covered thus far. To properly sketch a curve, you must analyze the function and its first and second derivatives in order to obtain information about how the function behaves, taking into account its intercepts, asymptotes (vertical and horizontal), maximum values, minimum values, points of inflection, and the respective intervals between each of the above. After collecting this information, you will need to piece it all together in order to sketch an approximation to the graph of the original function.
Completing this unit should take you approximately 10 hours.
Unit 6: Applications of the Derivative
With a sufficient amount of sophisticated machinery under your belt, you will now start to look at how differentiation can be used to solve problems in various applied settings. Optimization is an important notion in fields like biology, economics, and physics when we want to know when growth is maximized, for example.
In addition to providing methods to solve problems directly, the derivative can also be used to find approximate solutions to problems. You will explore two such methods in this section: Newton's method and the method of differentials.
Completing this unit should take you approximately 13 hours.
Unit 7: Integration
In this unit of the course, you will learn about integral calculus, a subfield of calculus that studies the area formed under the curve of a function. Though not necessarily intuitive, this concept is closely related to the derivative, which you will revisit in this unit.
Completing this unit should take you approximately 21 hours.
Unit 8: Applications of Integration
In this unit, we will take a first look at how integration can and has been used to solve various types of problems. Now that you have conceptualized the relationship between integration and areas and distances, you are ready to take a closer look at various applications; these range from basic geometric identities to more advanced situations in physics and engineering.
Completing this unit should take you approximately 19 hours.
Final Exam
Power, Product, and Quotient Rule Worksheet: odds Power, Product, and Quotient Rules Worksheet Power, Product, and Quotient Rules Worksheet Key page 206: 3-19 odd, 21, & 25 page 225: 1-11 odd, 17, 23, & 25. Practicing Derivative Rules II. View study plan. 2550 north lake drive suite 2 milwaukee, wi 53211. About privacy contact. Unit 2 (Chapter 3) - Derivatives posted Sep 19, 2012, 8:16 AM by Jim Bartuska updated Nov 17, 2014, 2:35 PM. Most of us last saw calculus in school, but derivatives are a critical part of machine learning, particularly deep neural networks, which are trained by optimizing a loss function. This article is an attempt to explain all the matrix calculus you need in order to understand the training of deep neural networks. We assume no math knowledge beyond what you learned in calculus 1, and provide. UNIT 3 - Basic Differentiation. 3.2 Product & Quotient Rule. 3.3 Velocity & other Rates of Change. 3.5 Trig Derivatives.
In the next few sections, we’ll get the derivative rules that will let us find formulas for derivatives when our function comes to us as a formula. This is a very algebraic section, and you should get lots of practice. When you tell someone you have studied calculus, this is the one skill they will expect you to have.
To view this video please enable JavaScript, and consider upgrading to a web browser that supports HTML5 video
Building Blocks
These are the simplest rules – rules for the basic functions. We won't prove these rules; we'll just use them. But first, let's look at a few so that we can see they make sense.
Example 1
Find the derivative of ( y=f(x)=mx+b )
This is a linear function, so its graph is its own tangent line! The slope of the tangent line, the derivative, is the slope of the line: [f'(x)=m]
Rule:
The derivative of a linear function is its slope.
To view this video please enable JavaScript, and consider upgrading to a web browser that supports HTML5 video
Example 2
Find the derivative of ( f(x)=135 ).
Think about this one graphically, too. The graph of f(x) is a horizontal line. So its slope is zero: [f'(x)=0]
To view this video please enable JavaScript, and consider upgrading to a web browser that supports HTML5 video
Example 3
Find the derivative of ( f(x)=x^2 ).
Recall the formal definition of the derivative: [f'(x)=limlimits_{hto 0} frac{f(x+h)-f(x)}{h}.]
Using our function ( f(x)=x^2 ), ( f(x+h)=(x+h)^2=x^2+2xh+h^2 ).
Then [ begin{align*} f'(x)=& limlimits_{hto 0} frac{f(x+h)-f(x)}{h} =& limlimits_{hto 0} frac{x^2+2xh+h^2-x^2}{h} =& limlimits_{hto 0} frac{2xh+h^2}{h} =& limlimits_{hto 0} frac{h(2x+h)}{h} =& limlimits_{hto 0} (2x+h) =& 2x end{align*} ]
From all that, we find that ( f'(x)=2x ).
Luckily, there is a handy rule we use to skip using the limit:
Power Rule
The derivative of ( f(x)=x^n ) is [f'(x)=nx^{n-1}.]
To view this video please enable JavaScript, and consider upgrading to a web browser that supports HTML5 video
To view this video please enable JavaScript, and consider upgrading to a web browser that supports HTML5 video
Example 4
Find the derivative of ( g(x)=4x^3 )
Using the power rule, we know that if ( f(x)=x^3 ), then ( f'(x)=3x^2 ). Notice that (g) is 4 times the function (f). Think about what this change means to the graph of (g) – it’s now 4 times as tall as the graph of (f). If we find the slope of a secant line, it will be ( frac{Delta g}{Delta x}= frac{4Delta f}{Delta x} =4frac{Delta f}{Delta x} ); each slope will be 4 times the slope of the secant line on the (f) graph. This property will hold for the slopes of tangent lines, too: [frac{d}{dx}left(4x^3right)=4frac{d}{dx}left(x^3right)=4cdot 3x^2=12x^2.]
Rule:
Constants come along for the ride, i.e., ( frac{d}{dx}left( kfright)=kf'.)
To view this video please enable JavaScript, and consider upgrading to a web browser that supports HTML5 video
Here are all the basic rules in one place.
Derivative Rules: Building Blocks
In what follows, (f) and (g) are differentiable functions of (x).
Constant Multiple Rule
[ frac{d}{dx}left( kfright)=kf']
Sum and Difference Rule
[frac{d}{dx}left(fpm gright)=f' pm g']
Power Rule
[frac{d}{dx}left(x^nright)=nx^{n-1}]
Special cases: [frac{d}{dx}left(kright)=0 quad text{(Because ( k=kx^0 ).)}] [frac{d}{dx}left(xright)=1 quad text{(Because ( x=x^1 ).)}]
Exponential Functions
[frac{d}{dx}left(e^xright)=e^x] [frac{d}{dx}left(a^xright)=ln(a),a^x]
Natural Logarithm
[frac{d}{dx}left(ln(x)right)=frac{1}{x}]
The sum, difference, and constant multiple rule combined with the power rule allow us to easily find the derivative of any polynomial.
To view this video please enable JavaScript, and consider upgrading to a web browser that supports HTML5 video
To view this video please enable JavaScript, and consider upgrading to a web browser that supports HTML5 video
Example 5
Find the derivative of ( p(x)=17x^{10}+13x^8-1.8x+1003 ).
[ begin{align*} frac{d}{dx}left( 17x^{10}+13x^8-1.8x+1003 right)=& frac{d}{dx}left( 17x^{10} right)+frac{d}{dx}left( 13x^8 right)-frac{d}{dx}left( 1.8x right)+frac{d}{dx}left( 1003 right) =& 17frac{d}{dx}left( x^{10} right)+13frac{d}{dx}left( x^8 right)-1.8frac{d}{dx}left( x right)+frac{d}{dx}left( 1003 right) =& 17left(10x^9right)+13left(8x^7right)-1.8left(1right)+0 =& 170x^9+104x^7-1.8 end{align*} ]
You don't have to show every single step. Do be careful when you're first working with the rules, but pretty soon you’ll be able to just write down the derivative directly:
Example 6
Find (frac{d}{dx}left( 17x^2-33x+12 right)).
Writing out the rules, we'd write [frac{d}{dx}left( 17x^2-33x+12 right)=17(2x)-33(1)+0=34x-33.]
Once you're familiar with the rules, you can, in your head, multiply the 2 times the 17 and the 33 times 1, and just write [frac{d}{dx}left( 17x^2-33x+12 right)=34x-33.]
The power rule works even if the power is negative or a fraction. In order to apply it, first translate all roots and basic rational expressions into exponents:
Example 7
Find the derivative of ( y=3sqrt{t}-frac{4}{t^4}+5e^t ).
The first step is translate into exponents: [y=3sqrt{t}-frac{4}{t^4}+5e^t=3t^{1/2}-4t^{-4}+5e^t]
Now you can take the derivative: [ begin{align*} frac{d}{dt}left( 3t^{1/2}-4t^{-4}+5e^t right)=& 3left(frac{1}{2}t^{-1/2}right)-4left(-4t^{-5}right)+5left(e^tright) =& frac{3}{2}t^{-1/2}+16t^{-5}+5e^t end{align*} ]
If there is a reason to, you can rewrite the answer with radicals and positive exponents: [y'= frac{3}{2}t^{-1/2}+16t^{-5}+5e^t= frac{3}{2sqrt{t}}+frac{16}{t^5}+5e^t]
Be careful when finding the derivatives with negative exponents.
We can immediately apply these rules to solve the problem we started the chapter with - finding a tangent line.
Unit 3 Derivative Rules Of Compositesap Calculus Integrals
Example 8
Find the equation of the line tangent to ( g(t)=10-t^2 ) when (t = 2).
The slope of the tangent line is the value of the derivative. We can compute ( g'(t)=-2t ). To find the slope of the tangent line when (t = 2), evaluate the derivative at that point. The slope of the tangent line is -4.
To find the equation of the tangent line, we also need a point on the tangent line. Since the tangent line touches the original function at (t = 2), we can find the point by evaluating the original function: ( g(2)=10-2^2=6 ). The tangent line must pass through the point (2, 6).
Using the point-slope equation of a line, the tangent line will have equation ( y-6=-4(t-2) ). Simplifying to slope-intercept form, the equation is ( y=-4t+14 ).
Graphing, we can verify this line is indeed tangent to the curve:
We can also use these rules to help us find the derivatives we need to interpret the behavior of a function.
Example 9
In a memory experiment, a researcher asks the subject to memorize as many words from a list as possible in 10 seconds. Recall is tested, then the subject is given 10 more seconds to study, and so on. Suppose the number of words remembered after (t) seconds of studying could be modeled by ( W(t)=4t^{2/5} ). Find and interpret ( W'(20) ).
( W'(t)=4cdot frac{2}{5}t^{-3/5}=frac{8}{5}t^{-3/5} ), so ( W'(20)=frac{8}{5}(20)^{-3/5}approx 0.2652 ).
Since (W) is measured in words, and (t) is in seconds, (W') has units words per second. ( W'(20)approx 0.2652 ) means that after 20 seconds of studying, the subject is learning about 0.27 more words for each additional second of studying.
Business and Economics Terms
Next we will delve more deeply into some business applications. To do that, we first need to review some terminology.
Suppose you are producing and selling some item. The profit you make is the amount of money you take in minus what you have to pay to produce the items. Both of these quantities depend on how many you make and sell. (So we have functions here.) Here is a list of definitions for some of the terminology, together with their meaning in algebraic terms and in graphical terms.
Cost
Your cost is the money you have to spend to produce your items.
Fixed Cost
The Fixed Cost (FC) is the amount of money you have to spend regardless of how many items you produce. FC can include things like rent, purchase costs of machinery, and salaries for office staff. You have to pay the fixed costs even if you don’t produce anything.
Total Variable Cost
The Total Variable Cost (TVC) for (q) items is the amount of money you spend to actually produce them. TVC includes things like the materials you use, the electricity to run the machinery, gasoline for your delivery vans, maybe the wages of your production workers. These costs will vary according to how many items you produce.
Total Cost
The Total Cost (TC, or sometimes just C) for (q) items is the total cost of producing them. It’s the sum of the fixed cost and the total variable cost for producing (q) items.
Average Cost
The Average Cost (AC) for (q) items is the total cost divided by (q), or (frac{TC}{q}). You can also talk about the average fixed cost, (frac{FC}{q}), or the average variable cost, (frac{TVC}{q}).
Marginal Cost
The Marginal Cost (MC) at (q) items is the cost of producing the next item. Really, it’s [MC(q) = TC(q + 1) - TC(q).] In many cases, though, it’s easier to approximate this difference using calculus (see Example 11 below). And some sources define the marginal cost directly as the derivative, [MC(q) = TC'(q).] In this course, we will use both of these definitions as if they were interchangeable.

The units on marginal cost is cost per item.
Why is it okay that there are two definitions for Marginal Cost (and Marginal Revenue, and Marginal Profit)?
We have been using slopes of secant lines over tiny intervals to approximate derivatives. In this example, we’ll turn that around – we’ll use the derivative to approximate the slope of the secant line.
Notice that the “cost of the next item” definition is actually the slope of a secant line, over an interval of 1 unit: [MC(q) = C(q + 1) - 1 = frac{C(q+1)-1}{1}.]
So this is approximately the same as the derivative of the cost function at q: [MC(q) = C'(q).]
In practice, these two numbers are so close that there’s no practical reason to make a distinction. For our purposes, the marginal cost is the derivative is the cost of the next item.
Example 10
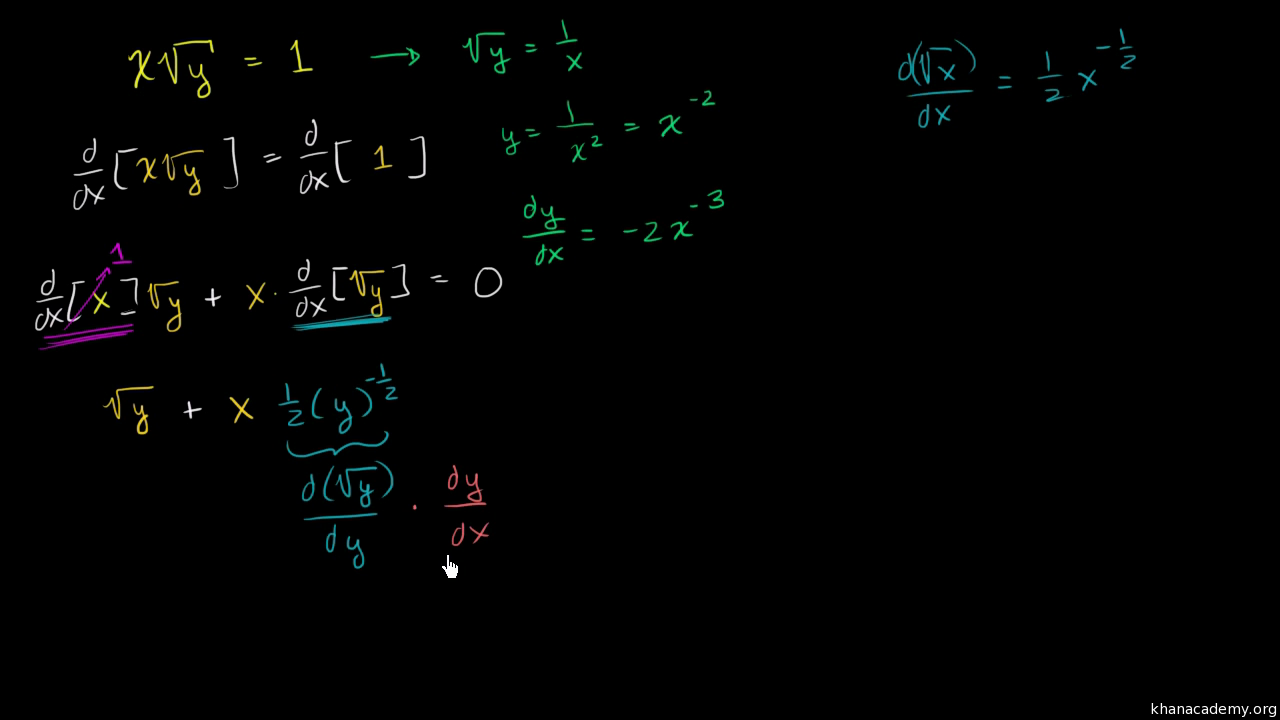
The table shows the total cost (TC) of producing (q) items.
| Items, ( q ) | TC |
| 0 | $20,000 |
| 100 | $35,000 |
| 200 | $45,000 |
| 300 | $53,000 |
- What is the fixed cost?
- When 200 items are made, what is the total variable cost? The average variable cost?
- When 200 items are made, estimate the marginal cost.
- The fixed cost is $20,000, the cost even when no items are made.
When 200 items are made, the total cost is $45,000. Subtracting the fixed cost, the total variable cost is $45,000 - $20,000 = $25,000.
The average variable cost is the total variable cost divided by the number of items, so we would divide the $25,000 total variable cost by the 200 items made. $25,000/200 = $125. On average, each item had a variable cost of $125.
We need to estimate the value of the derivative, or the slope of the tangent line at (q = 200). Finding the secant line from (q=100) to (q=200) gives a slope of [ frac{45,000-35,000}{200-100}=100.]
Finding the secant line from (q=200) to (q=300) gives a slope of [frac{53,000-45,000}{300-200}=80.]
We could estimate the tangent slope by averaging these secant slopes, giving us an estimate of $90/item.
This tells us that after 200 items have been made, it will cost about $90 to make one more item.
To view this video please enable JavaScript, and consider upgrading to a web browser that supports HTML5 video

Example 11
The cost to produce (x) items is (sqrt{x}) hundred dollars.
- What is the cost for producing 100 items? 101 items? What is cost of the 101st item?
- For (f(x) = sqrt{x}), calculate (f '(x)) and evaluate (f ') at (x = 100). How does (f '(100)) compare with the last answer in Part a?
- Put (f(x) = sqrt{x} = x^{1/2})hundred dollars, the cost for (x) items. Then (f(100) =)$1000 and (f(101) =)$1004.99, so it costs $4.99 for that 101st item. Using this definition, the marginal cost is $4.99.
- ( f'(x)=frac{1}{2}x^{-1/2}), so ( f'(100)=frac{1}{2sqrt{100}}=frac{1}{20} ) hundred dollars = $5.00.
Note how close these answers are! This shows (again) why it’s OK that we use both definitions for marginal cost.
Demand
Demand is the functional relationship between the price (p) and the quantity (q) that can be sold (that is demanded). Depending on your situation, you might think of (p) as a function of (q), or of (q) as a function of (p)
Revenue
Your revenue is the amount of money you actually take in from selling your products.
The Total Revenue (TR, or just R) for (q) items is the total amount of money you take in for selling (q) items. Total Revenue is price multiplied by quantity, [TR = p cdot q.]
Unit 3 Derivative Rules Of Compositesap Calculus Solver
Average Revenue
The Average Revenue (AR) for (q) items is the total revenue divided by (q), or [frac{TR}{q}.]
Marginal Revenue
The Marginal Revenue (MR) at (q) items is the revenue from producing the next item, [MR(q) = TR(q + 1) - TR(q).]
Just as with marginal cost, we will use both this definition and the derivative definition: [MR(q) = TR'(q).]
Profit
Your profit is what’s left over from total revenue after costs have been subtracted.
The Profit (P) for (q) items is [TR(q) - TC(q),] the difference between total revenue and total costs.
The average profit for (q) items is [frac{P}{q}.]
The marginal profit at (q) items is [P(q + 1) – P(q),] or [P'(q)]
To view this video please enable JavaScript, and consider upgrading to a web browser that supports HTML5 video
Graphical Interpretations of the Basic Business Math Terms
Illustration
Here are the graphs of TR and TC for producing and selling a certain item. The horizontal axis is the number of items, in thousands. The vertical axis is the number of dollars, also in thousands.
First, notice how to find the fixed cost and variable cost from the graph here. FC is the (y)-intercept of the TC graph. ((FC = TC(0)).) The graph of TVC would have the same shape as the graph of TC, shifted down. ((TVC = TC - FC).)
Unit 3 Derivative Rules Of Compositesap Calculus Calculator
(MC(q) = TC(q + 1) - TC(q)), but that’s impossible to read on this graph. How could you distinguish between TC(4022) and TC(4023)? On this graph, that interval is too small to see, and our best guess at the secant line is actually the tangent line to the TC curve at that point. (This is the reason we want to have the derivative definition handy.)
(MC(q)) is the slope of the tangent line to the TC curve at ( (q, TC(q))).
(MR(q)) is the slope of the tangent line to the TR curve at ((q, TR(q))).
Profit is the distance between the TR and TC curve. If you experiment with a clear ruler, you’ll see that the biggest profit occurs exactly when the tangent lines to the TR and TC curves are parallel. This is the rule profit is maximized when ( MR = MC)
which we'll explore later in the chapter.
Example 12
The demand, (D), for a product at a price of (p) dollars is given by ( D(p)=200-0.2p^2 ). Find the marginal revenue when the price is $10.
First we need to form a revenue equation. Since Revenue = Price( times )Quantity, and the demand equation shows the quantity of product that can be sold, we have [R(p)=D(p)cdot p=left(200-0.2p^2right)p=200p-0.2p^3.]
Now we can find marginal revenue by finding the derivative: [R'(p)=200(1)-0.2(3p^2)=200-0.6p^2]
At a price of $10, ( R'(10)=200-0.6(10)^2=140 ).
Unit 3 Derivative Rules Of Compositesap Calculus 2nd Edition
Notice the units for (R') are (frac{text{dollars of Revenue}}{text{dollar of price}}), so ( R'(10)=140 ) means that when the price is $10, the revenue will increase by $140 for each dollar that the price was increased.
